深度学习-李沐-第三节-SoftMax
SoftMax
疑点难点:
损失函数、代码实现
理解
- softmax运算获取一个向量并将其映射为概率。
- softmax回归适用于分类问题,它使用了softmax运算中输出类别的概率分布。
- 交叉熵是一个衡量两个概率分布之间差异的度量
回归与分类
- 回归估计一个连续值
- 分类预测一个离散类别

网络架构
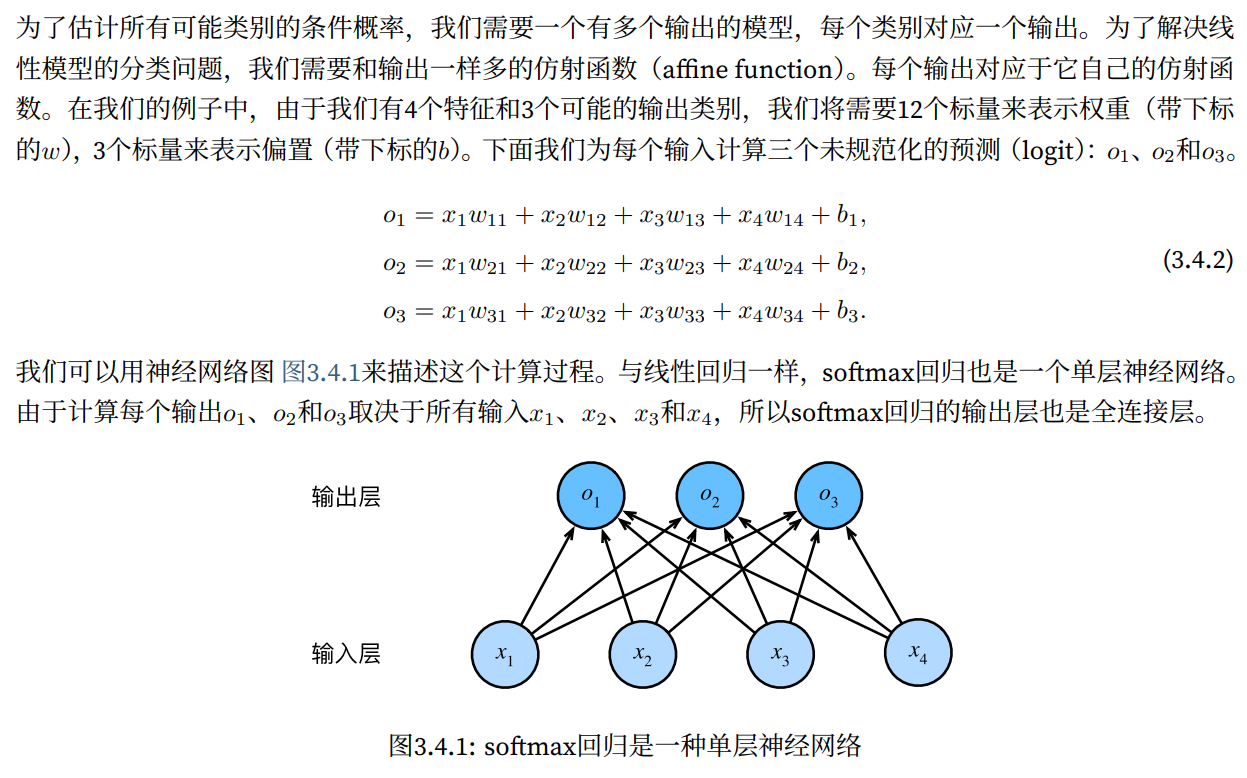
从回归过渡到多类分类
- 均方损失
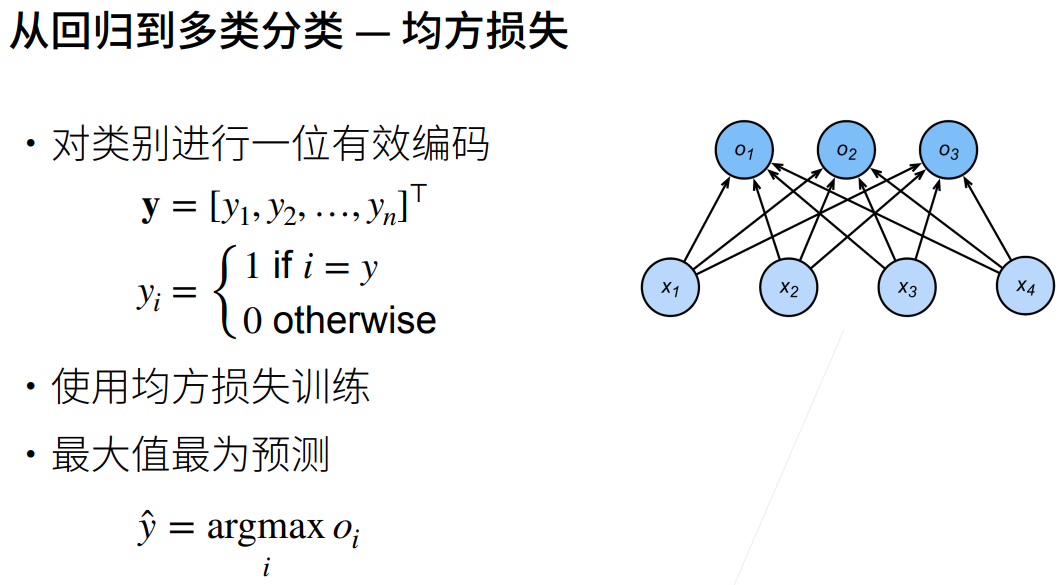
- 无校验比例
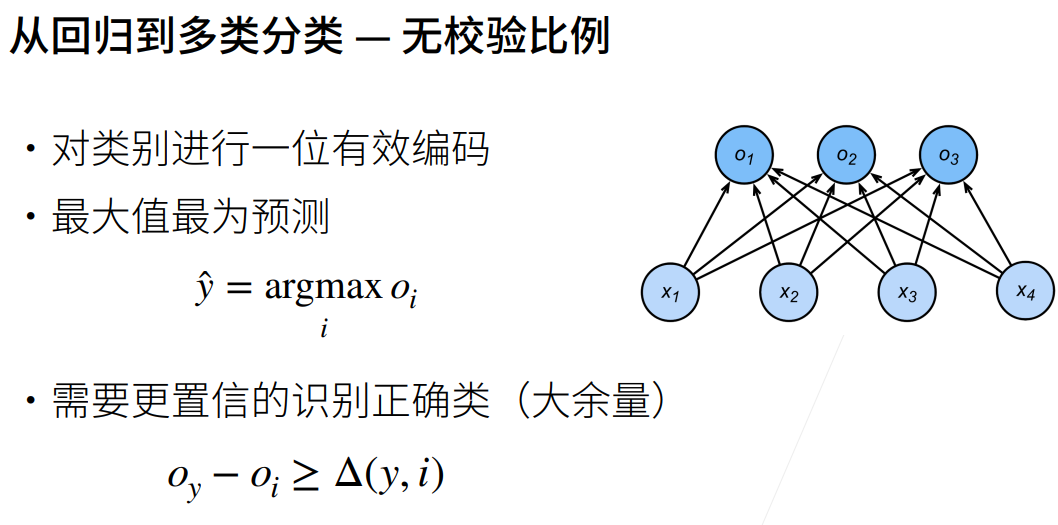
- 校验比例
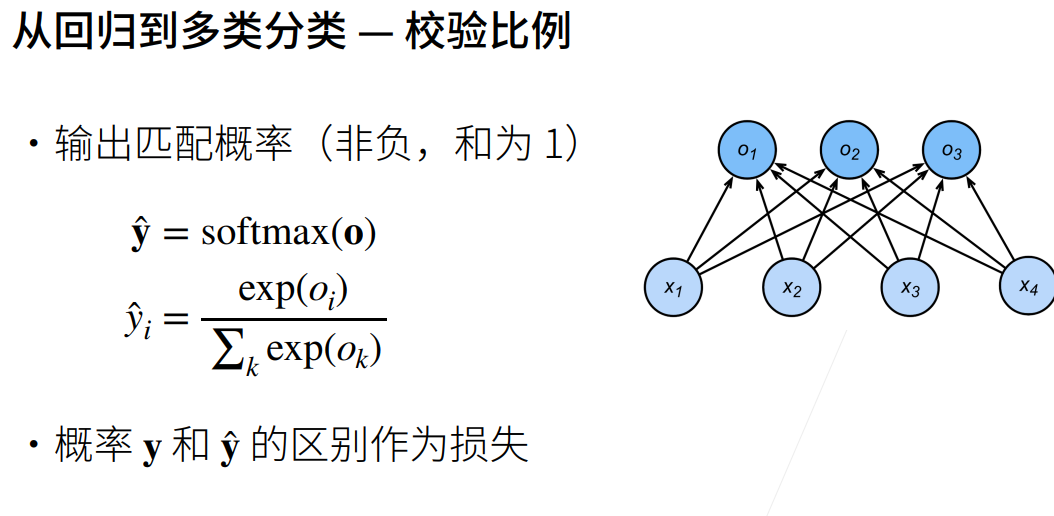
损失函数
两种损失函数:
L2 Loss: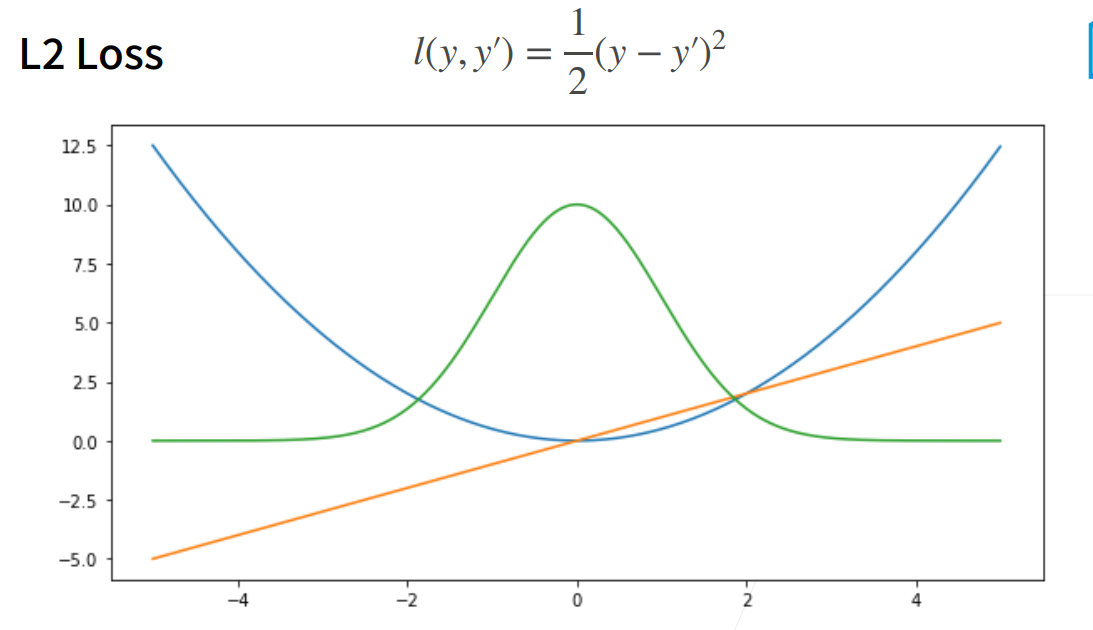
L1 Loss: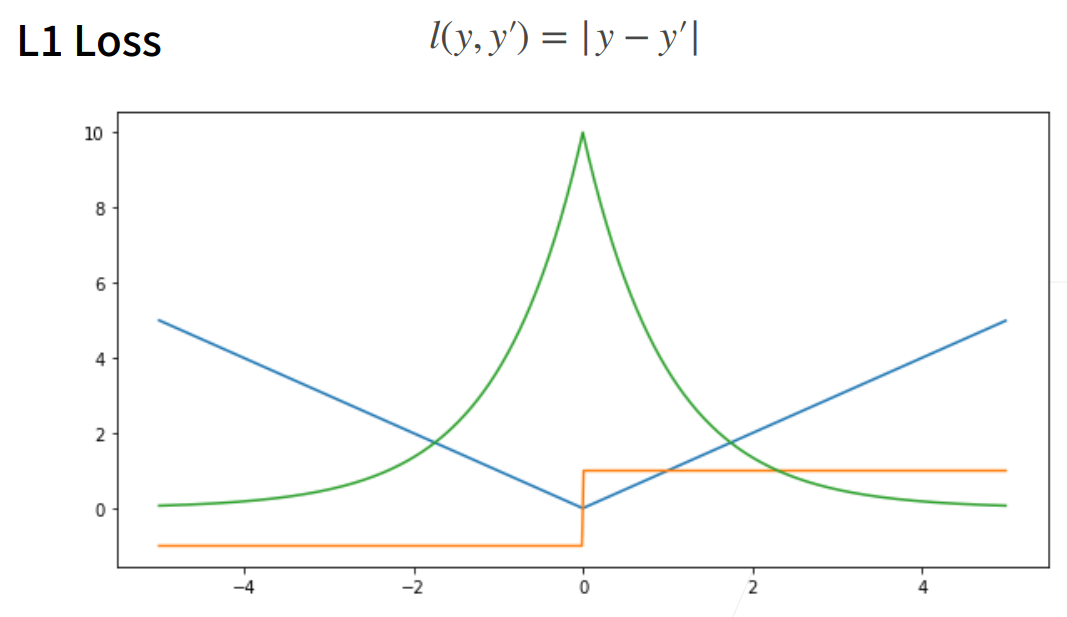
交叉熵
交叉熵用来判定实际的输出与期望的输出的接近程度
交叉熵刻画的是实际输出(概率)与期望输出(概率)的距离,也就是交叉熵的值越小,两个概率分布就越接近。
在二分类的基础上,交叉熵有更通用的表达形式,因为二分类只是分类问题的特例,更多的还是多分类问题。通用的交叉熵要对应Softmax函数使用,所以有时候Softmax+交叉熵也被称为Softmax损失函数,它表达式为:
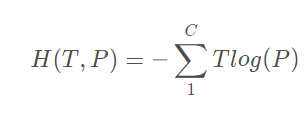
模型评估
在训练softmax回归模型后,给出任何样本特征,通常我们使用预测概率最高的类别作为输出类别。
如果预测与实际类别(标签)一致,则预测是正确的。使用精度(accuracy)来评估模型的性能。
精度等于正确预测数与预测总数之间的比率。